Piecewise affine functions

Affine function: $f (x) = A * x + b$
Piecewise Affine function:

f (x) = {\begin{cases} - x - 5, & if x <= - 3 \\ x + 23, & if - 3 < x <= 2 \\ 4 * x + 7, & if 2 < x \end{cases}

Why Relu layers create piecewise affine function

Linear layers: $f (x) = w * x + b$ , simply an affine function
Relu Layers:

f (x) = {\begin{cases} 0, & if x < 0 \\ x & otherwise \end{cases}

Therefore a ReLU neural network is simply an affine function with a high number of "pieces".

Why Piece-wise affine functions are always overconfident if far away from the data.

If you move far away into one direction, at some point you will stay in a linear space until infinity (following that direction). Therefore at some point you will approach either 0 or 100% class probability, therefore 100% confidence in your prediction.

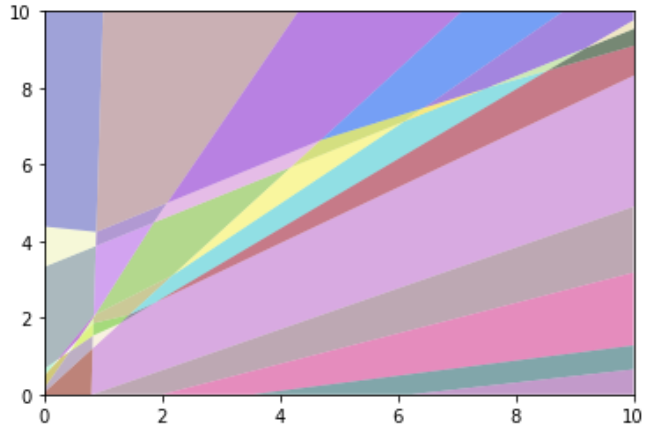
Pasted image 20240620154729.png

The coloured areas are the affine parts. Ignore the white dotted lines.

Why this cannot be fixed with temperature scaling.

Temperature scaling is a post processing technique to make neural networks calibrated. It divides the the logits vector (neural network output) by a learnt scalar parameter. Since our theory is valid for any $ϵ > 0$ , dividing by a scalar does not fix the problem.

Why this cannot be fixed with Softmax:

σ (z)_{i} = \frac{e^{z_{i}}}{\sum_{j = 1}^{K} e^{z_{j}}}

This does not change the relative magnitude of the logits. So if the original distribution is heavily skewed, then the softmax distribution will be as well.

How to fix it?

One idea are Bayesian Neural Networks networks. But basically the problem is unsolved.

Github example

https://github.com/philippweinmann/Uncertainty_in_ml