Graph representation

Graphs have the following properties

Nodes: Representing entities
Edges: Representing relationships or interactions

Both edges and nodes usually have associated features

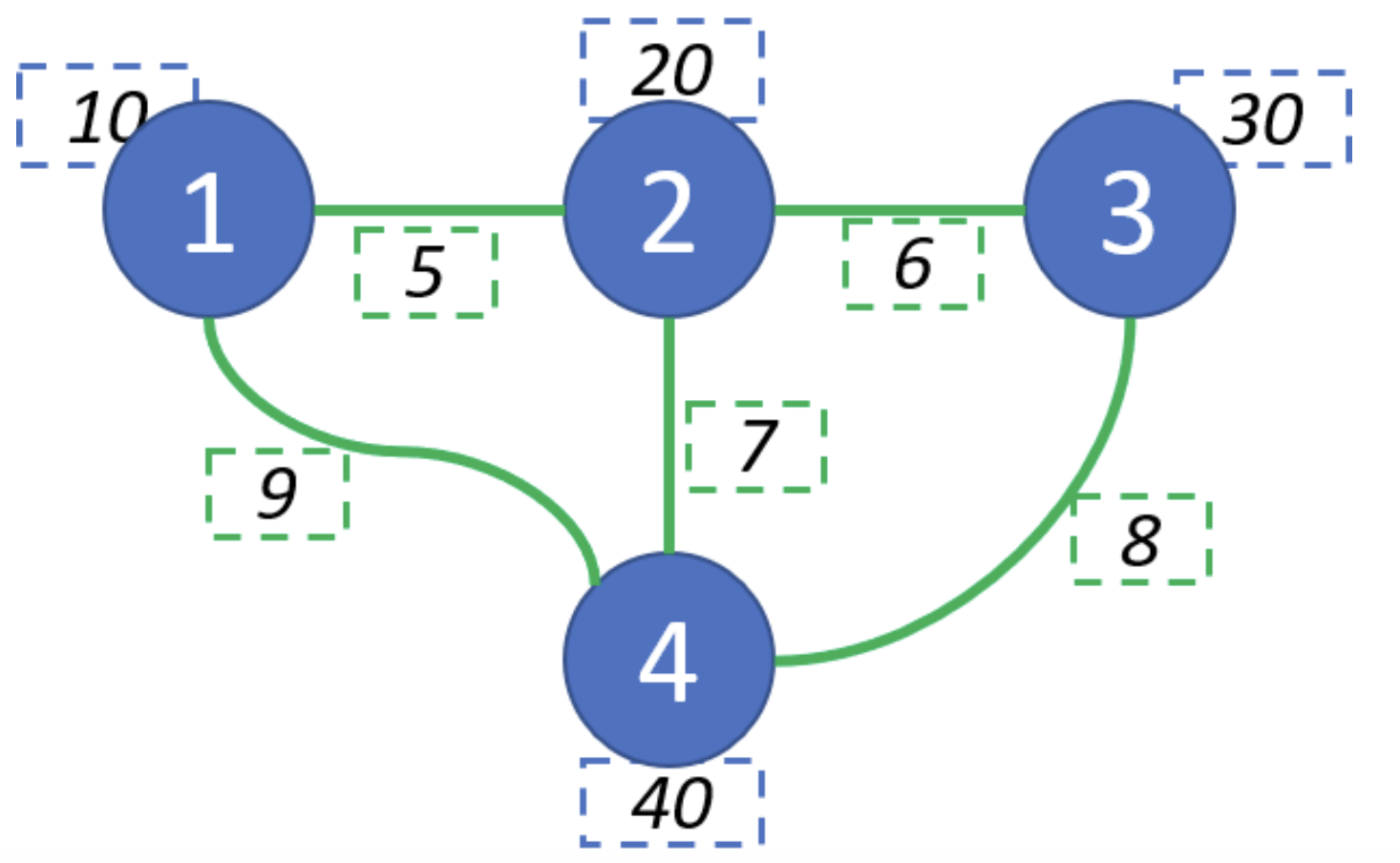
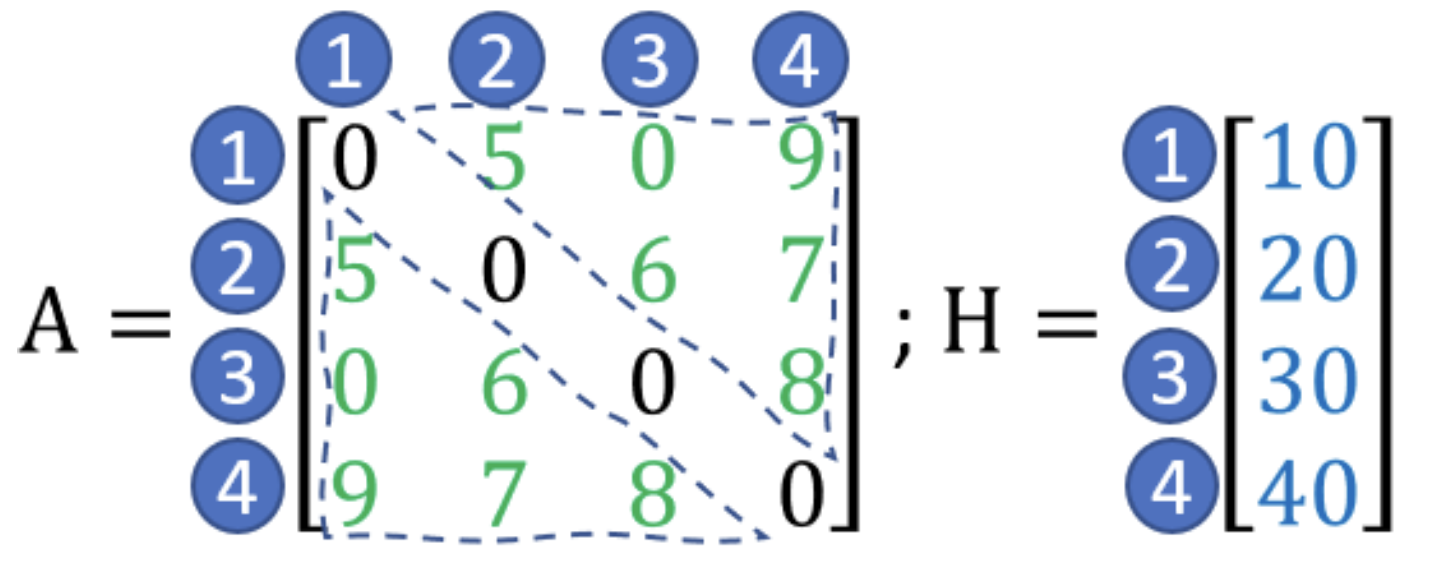
How is a graph saved in matrix form?

Pasted image 20250311133050.png

notice the symmetry of the adjacency (edge) matrix due to the fact that the graph is not directed.

Pasted image 20250311133101.png

most numerical graph representations involve more steps, like normalization and more

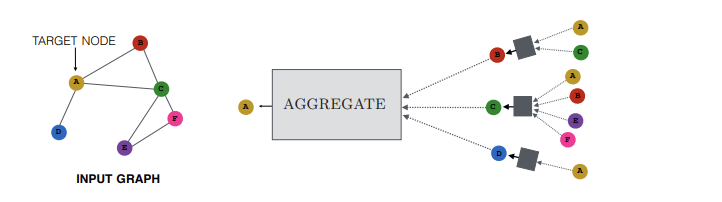
Core idea

I believe there are more ways to accumulate local graph information, but I haven't checked them out.

message passing

The model looks at each node and its "neighbors". It then creates an embedding of the local view of that node and "sends" it to its local neighbors. The nodes then collect those messages and aggregate them. After doing that this node can then combine its current embedding with the aggregated messages to produce a new embedding.

This process called message passing happens in the message passing layers.

While initially only getting information from immediate neighbours, the more times this process is repeated, the more information from nodes further away we're getting.

Why use such an update strategy?

in the end it is always about beating the curse of dimensionality. In this case, like in most, by the use of scale separation and equivariance.

Graphs, as opposed to images or other types of data do not have regular data, in the sense it is not in the form of a grid. Therefore, filters like they are used in CNNs cannot be directly applied.

We follow the idea of Scale separation, ml architecture context, with this strategy. First we look at the nodes themselves, their immediate neighbourhood and gradually increase the receptive field.

The assumption, that close neighbours have a stronger influence than further away ones is encoded in the model training process like this. This assumption is almost always correct.

Permutation variance: Since graphs have no inherent node ordering, message-passing is actually a permutation invariant aggregation. This flows into the whole context of How to think about model architecture#Equivariance.

Pytorch implementation

from torch_geometric.nn import GCNConv
import torch

class SocialGNN(torch.nn.Module):
    def __init__(self,num_of_feat,f):
        super(SocialGNN, self).__init__()
        self.conv1 = GCNConv(num_of_feat, f)
        self.conv2 = GCNConv(f, 2)

    def forward(self, data):
        x = data.x.float()
        edge_index =  data.edge_index
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = self.conv2(x, edge_index)
        return x

The {python}GCNConvlayers constitute the message passing explained above.

if we added more {python}GCNConvLayers, then we would incorporate more information from surrounding nodes. While this might add some useful information, there are tradeoffs.

Too many {python}GCNConvLayers can lead to:

Over smoothing: All node representations will looks similar. It works like a kinda blur.

Divers

Definitions

General Attributed Graph: A graph in which nodes, edges or the entire graph can carry additional features or attributes.