The original dice loss does not consider the output values of classification problems, but post processes them into binary or n-ary images using probability thresholds. Threfore I consider the base dice loss trash.

The Dice Loss is based on the dice coefficient, a different way to measure the accuracy of a prediction/model.

(soft) Dice coefficient

in practice the prediction are probability scores. For binary classification problems we can define the overlap as 2 * y_pred * y_true, y_pred being the probability score.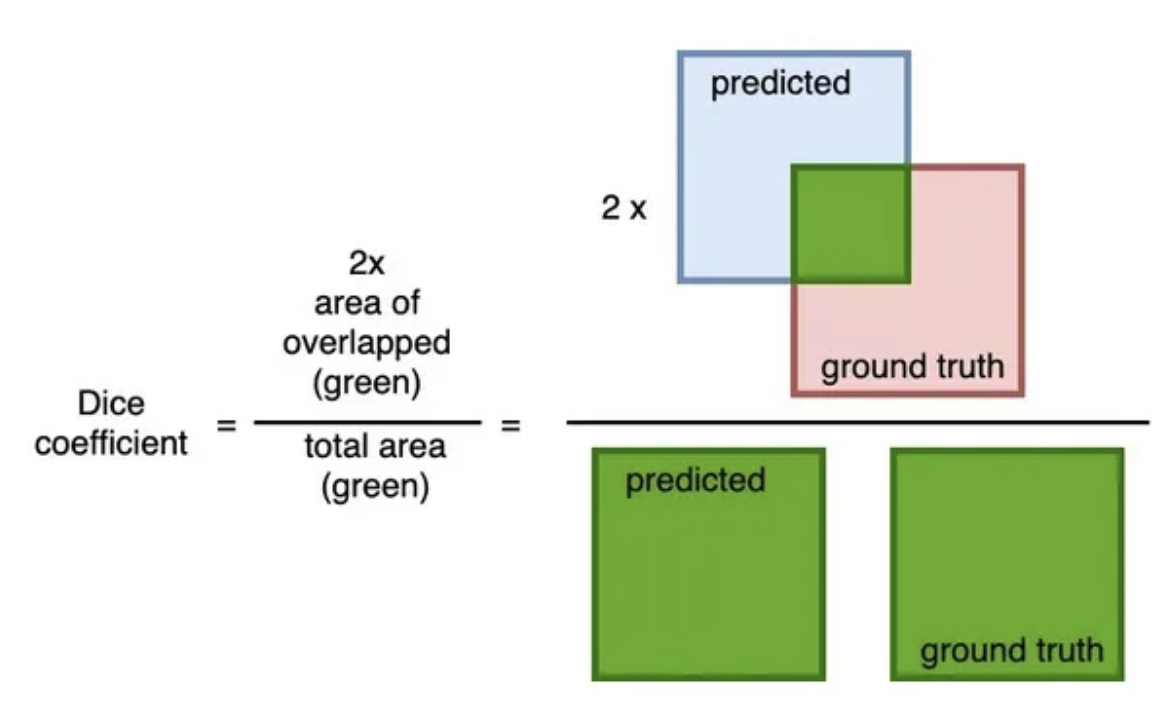

Pasted image 20241112103936.png

Goal

The dice coefficient is useful in the following cases:

Imbalanced classes: If we have a heavily unbalanced problem, where one class clearly dominates, then traditional accuracy measures (like Cross entropy) fail at capturing the actual accuracy of the model. By simply returning the dominant class, we would get a high accuracy score even though we haven't solved the task at all.
When we want to measure the area of overlap. If this is more important than the differences, then the dice coefficient is a good choice.

both of these points often apply to (Semantic) Image Segmentation, especially in the medical field.

When not to use it

If the notion of overlap doesn't make any sense. For example in Regression problems, or any other kind of continuous data outputs.
If the overlap between the prediction and ground truth is not that important.

The Jaccard index can actually be calculated from the dice coefficient. The dice coefficient puts even more importance on the overlap and can therefore be considered more "agressive"

(Soft) Dice Loss

DiceLoss = 1 - DiceCoefficient

Own implementation, not guaranteed to be correct

def softdiceloss(predictions, targets, smooth: float = 0.00001):
    batch_size = targets.shape[0]
    intersection = (predictions * targets).view(batch_size, -1).sum(-1)

    targets_area = targets.view(batch_size, -1).sum(-1)
    predictions_area = predictions.view(batch_size, -1).sum(-1)

    dice = (2. * intersection + smooth) / (predictions_area + targets_area + smooth)

    return 1 - dice.mean()

Potential issues

Potential Instability: softdice loss can be unstable if the predicted areas are small (division by zero).

It can be an option to combine this loss and another loss to remedy the instability combined soft dice and cross entropy loss