this is just one aspect of the curse of dimensionality, there are others like similarity based approaches in high dimensional space
As the number of features/dimensions grows, the amount of data we need to generalize accurately grows exponentially.
One way to think about the curse of dimensionality in this context is interpolation. You have some points and you are trying to find a function that most likely passes through all those points. If the points become more "sparse" as is the case for high dimensions (and finite training points), interpolation becomes much harder.
Hughes/Peaking phenomenon:
With a fixed number of training samples, the average (expected) predictive power of a classifier or regressor first increases as the numbers of dimensions or features is used is increased but beyond a certain dimensionality, the accuracy starts deteriorating.
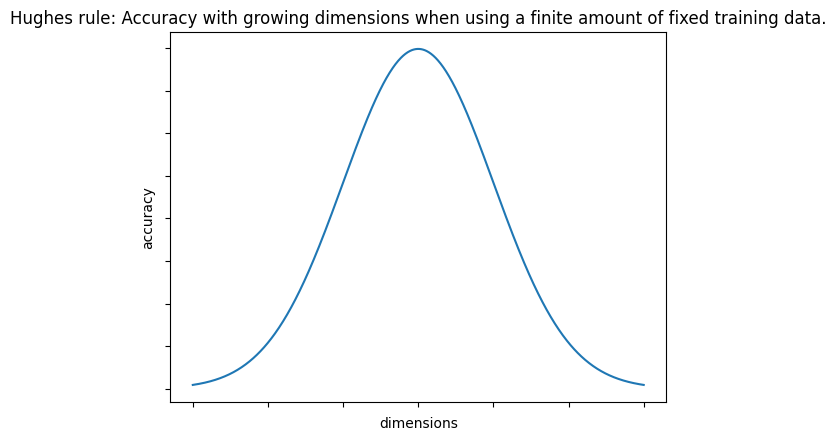
the higher the dimensions, the more "sparse" the data becomes.